| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 링커
- eigenvalue
- linear algebra
- 정보처리기사 2025 1회 실기 벼락치기
- column space
- 정처기 공부법
- 컴퓨터밑바닥의비밀
- 재배치
- 구문트리
- CS정리
- 코드포스
- 대상파일
- 스레드전용저장소
- Rust
- 정보처리기사 실기 벼락치기
- 선형대수학
- 다이나믹 프로그래밍
- unity
- matrix
- rust 스터디
- 벡터
- 다익스트라
- c++
- 컴파일러
- 정처기 실기 벼락치기
- 알고리즘
- vector
- 행렬
- 정처기 실기 공부법
- 백준
- Today
- Total
개발_기록용
[선형대수학 정리] 9. 행렬의 rank 본문
1. 배경
그래픽스 공부에 들어가기 전, 근본 중에서도 근본인 선형대수학을 먼저 파야겠다고 생각했다!
Chris Ohk 님의 Game Developer Roadmap 2022를 보고 내가 부족한 부분을 채워나가기로 결심했기 때문이다.
https://github.com/utilForever/game-developer-roadmap
GitHub - utilForever/game-developer-roadmap: Roadmap to becoming a game developer in 2022
Roadmap to becoming a game developer in 2022. Contribute to utilForever/game-developer-roadmap development by creating an account on GitHub.
github.com
2. 정리

rank : 행렬이 가지는 independent한 column의 수
앞서 살펴본 것처럼행렬에서 independent한 column의 수가 2개면, 2차원을 span할 수 있다.
이는 곧 rank = 2일 때, column space의 dimension이 2차원 이라는 의미이다.

그리고, 행렬에서 independent한 column의 수는
곧 independent한 row의 수와 같다.
따라서, rank는 row space의 dimension 이기도 하며
$$rank(A) = rank(A^{T})$$ 가 성립한다.

위의 행렬을 예시로 살펴보자.
첫번째 행렬은 세 column이 모두 평행하니 dependent하다.
즉, column space는 2x3 행렬이니 2차원에서 1차원을 span한다.
따라서, rank = 1
2차원 공간에서 1차원만 span하는 것처럼 rank가 주어진 공간보다 작으면 rank-deficient라 한다.
두번째 행렬은 세 column이 모두 independent하다.
그러나 2x3 행렬이니 2차원 공간이므로, row space 관점에서 2차원만 span한다.
따라서, rank = 2
m x n 행렬에서 rank가 row 수 m 과 같으면 full row rank 라 한다.
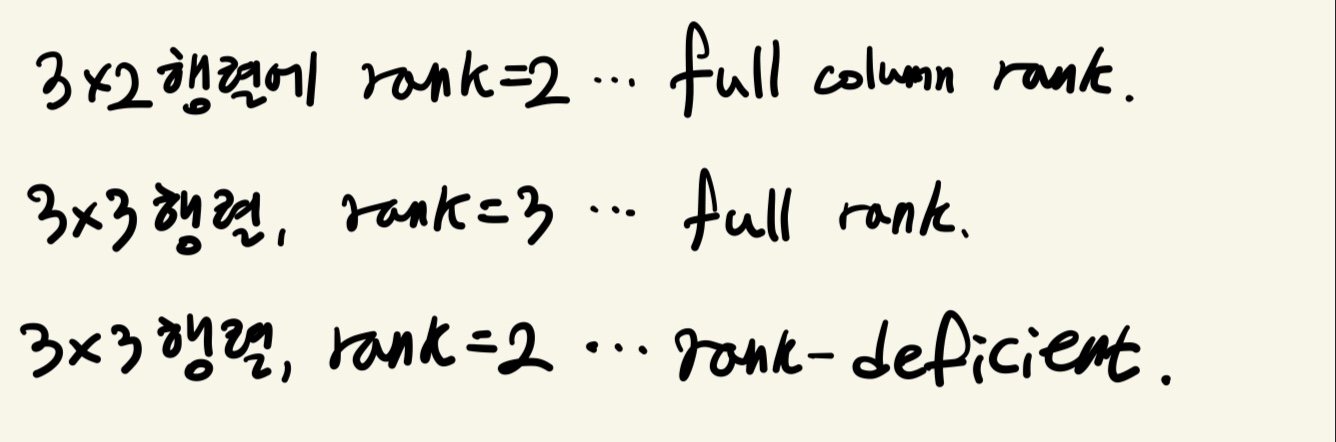
full row rank vs full column rank
full row rank를 방금 잠깐 봤기 때문에 헷갈릴 수 있어서 위의 예시들을 같이 살펴보자.
첫번째 행렬은 3x2 행렬인데 rank = 2이다.
column 수와 rank가 2로 같으므로, 이 경우 full column rank이다.
두번째 행렬은 3x3 행렬인데 rank = 3이다.
column 수와 row 수, rank가 모두 3으로 같으니, 이 경우 full rank라 한다.
반면 2x3 행렬인데 rank = 2라면
row 수와 rank가 2로 같으므로, 이 경우 full row rank이다.
마지막 행렬은 3x3 행렬인데 rank = 2로
row 수와 column 수보다 row가 작다. 이 경우 rank-deficient라 한다.
'선형대수학' 카테고리의 다른 글
| [선형대수학 정리] 11. Left Null Space (2) | 2024.07.19 |
|---|---|
| [선형대수학 정리] 10. Null space (0) | 2024.07.19 |
| [선형대수학 정리] 8. 대각행렬과 직교행렬 (0) | 2024.07.18 |
| [선형대수학 정리] 7. 항등행렬과 역행렬 (0) | 2024.07.18 |
| [선형대수학 정리] 6. Column space와 span (3) | 2024.07.16 |




