[선형대수학 정리] 23. 유사행렬 (Similar matrix)

1. 배경

 

---

그래픽스 공부에 들어가기 전, 근본 중에서도 근본인 선형대수학을 먼저 파야겠다고 생각했다!
 
Chris Ohk 님의 Game Developer Roadmap 2022를 보고 내가 부족한 부분을 채워나가기로 결심했기 때문이다.
 

https://github.com/utilForever/game-developer-roadmap

.

2. 정리

---

유사행렬 (Similar matrix)

 

 

정의) n x n 정방행렬 A에 대해

B = PAP^{-1}을 만족하는 n x n 행렬 P가 존재하면
A와 B는 유사행렬이다.

 

유사행렬의 property

 

조금 생소한 내용이긴 하지만 유용한 property가 많다.어떤 성질들인지 하나씩 살펴보자.

---

 

 

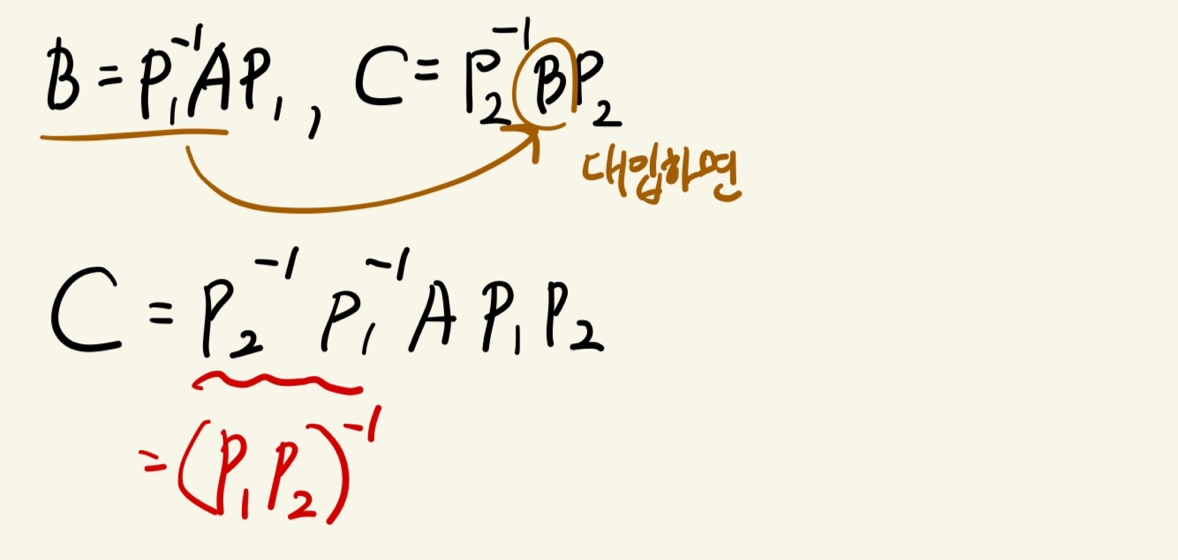
① A는 스스로 Similar 하다. 

→ 이때의 P를 구해보면 P = I 이다.

② B가 A와 Simliar하면 A도 B와 Similar 하다.

→ B = P^{-1}AP인 P가 존재하면 양변에 P^{-1}P를 곱해 A = P^{-1}BP임을 확인.

③ A와 B가 Similar 하고, B와 C가 Similar 하면 A와 C도 Similar 하다.

→ B의 유사행렬 식에 대해 C에 이를 대입하면 A에 대한 유사행렬 식이 나옴.

---

 

④ A와 B가 Similar 하면 rank(A) = rank(B)

→ P가 full rank면 P의 역행렬도 full rank이므로, 가장 작은 A의 rank를 따른다.

⑤ A와 B가 Similar 하면 tr(A) = tr(B)

→ trace의 circular property를 쓰면 P와 P의 역행렬이 지워져 A와 B의 trace가 같다.

---

 

⑥ A와 B가 Similar 하면 det(A) = det(B)

→ determinant는 곱의 형태로 쪼갤 수 있고, 역행렬의 det는 원래 행렬의 det의 역수이므로 이를 정리하면 A와 B의 det 값이 동일하다.

⑦ A와 B가 Similar 하면 고윳값도 같다.

→ Av = λv 에서 양변에 P^{-1}PP^{-1}을 곱하면 B의 고윳값도 λ로 같음을 알 수 있다.

 

(고유벡터는 A가 v라면 B는 P^{-1}v로 다르다.)

⑧ A와 B가 Similar 하면 A의 n제곱과 B의 n제곱도 Similar 하다.

→ B를 제곱하면 P와 P의 역행렬이 만나 지워지고, A의 제곱이 남아 서로 유사행렬임을 확인할 수 있다.